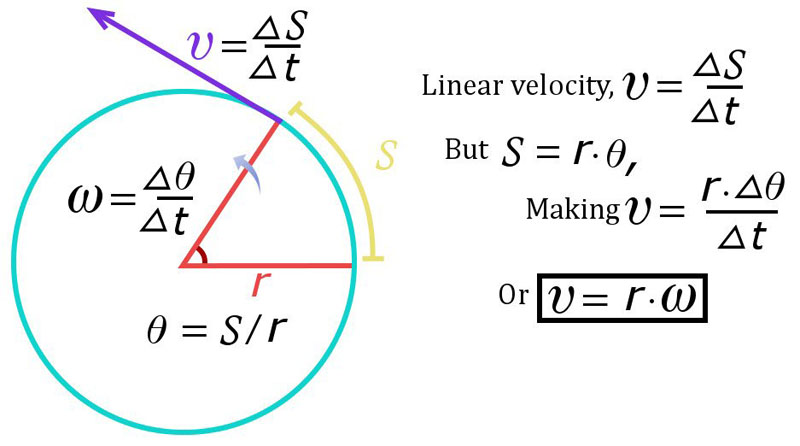OPENING QUESTIONS:

1) Explain the key to solving the ferris wheel problem to your group. Make sure you understand why we use mv²/r to describe the resulting motion of the person, but we do NOT include it in the sum-of-the-forces part of the equation.

2) If a space station completes one revolution in 23.5 seconds to simulate 1.00 g of acceleration on Earth, what is the circumference of the space station?

═══════════════════════════

We can measure the velocity of an object moving in a circular fashion by two methods. The first is how we might expect using units of meters and seconds:

We can pick a point at some distance (r) from the center, and determine how far that objects travels (in meters) and divide that by the time it takes to make one trip around (in seconds). The units of measure are our friendly ol' meters/sec.

So, let's say that we tether a small ball to the center of a record player a distance (r) from the center of that record player.

We know the distance (2πr) that ball travels each rotation of the player, and we can measure how long it takes to make one rotation. Divide the distance traveled by the time and VOILA.... easy sneezy-- the rotational velocity of the object in meters per second.

Now let's imagine we have that ball moving as before, but this time, we instantly cut the string. The ball will fly off into space in a LINEAR fashion at that same speed in a direction tangent to the circular motion at the instant the chord was cut. Hence the term tangential velocity.

We always measure tangential velocity in m/s.

The second method that we can use to measure circular motion is to measure how much an arc is swept out by the circular motion over time.

2π radians indicates one full rotation as we would expect.

Therefore, such 'angular' speed is measured in the number of radians (or fraction thereof) swept out each second and is given the term ω.

We can equate the radial speed of an object in radians per second to its speed in meters/sec by:

v = rω

We can get paralyzed by all the different terms. However, the important aspects to remember are these:

• We can measure the rotation of an object based on how far it rotates (in meters) divided by the time (in seconds) it takes to rotate.

• If an object is flung out of rotational motion it will continue moving in a straight line at that same speed ("linear velocity" in the image above)

• We can measure the rotation of an object based on how much an angle (measured in radians) is swept out per second.

• Those two types of measurement are related by the formula:

v = rω

═══════════════════════════

Now let's talk acceleration.

From http://www.softschools.com/formulas/physics/tangential_acceleration_formula/33/

"In rotational motion, tangential acceleration is a measure of how quickly a tangential velocity changes. It always acts perpendicular to the centripetal acceleration of a rotating object. It is equal to the angular acceleration α, times the radius of the rotation"

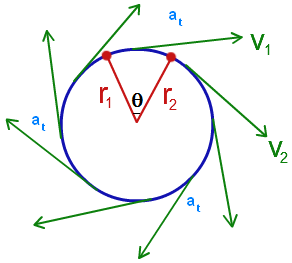
We are particularly interested in centripetal acceleration (a_c) which is the acceleration directed towards the center of the circular motion. We can measure that directly as v²/r where v is the velocity in m/s and r is the radius.

We are also interested in how an object moving in a circle's position changes over time, we often refer to that as the tangential acceleration. Notice that we find that the same way -- v²/r Why is that?

As with velocity, we can also measure acceleration in terms of the change in angular speed (ω) over time. Angular acceleration is represented by the Greek letter alpha (α).

We can relate angular acceleration to acceleration measured in m/s (either centripetal or tangential) by:

a = rω²

Consider this problem:

A small wheel speeds up with tangential acceleration a at a distance r from its center. A large wheel has a tangential acceleration of  2a  at a distance of  2r from its center.

How does the angular acceleration of the small wheel  α_small compare with the large wheel  α_large?